Cara Mengurutkan Pecahan : Matematika Kelas VII MTs Muhammadiyah 1 Muntilan
Pecahan adalah bilangan yang tidak utuh, terpecah atau terbagi. Pecahan ditulis dalam bentuk pembilang dan penyebut.
1. Mengurutkan pecahan dengan penyebut yang sama
Perhatikan garis bilangan berikut !
2. Mengurutkan pecahan dengan pembilang yang sama
Pembilang dalam pecahan bisa dianggap juga sebagai pembagi. Jika suatu bilangan yang sama dibagi angka yang lebih besar tentu menghasilkan nilai yang lebih kecil.
Contoh:
8 artinya 8 : 8 = 1
8
8 artinya 8 : 4 = 2
4
8 artinya 8 : 2 = 4, dan
2
8 artinya 8 : 1 = 8
1
Bisa kita lihat bahwa semakin kecil penyebut atau pembagi, maka nilai bilangan akan semakin besar. Jadi bisa kita simpulkan bahwa, untuk pecahan-pecahan dengan pembilang yang sama nilainya akan semakin besar jika penyebutnya semakin kecil.
3. Mengurutkan dua pecahan
Jika dua pecahan yang akan diurutkan memiliki penyebut yang sama atau pembilang yang sama, maka aturan yang sudah dibahas sebelumnya berlaku. Tapi jika dua pecahan yang akan diurutkan memiliki pembilang maupun penyebut yang berbeda bisa kita lakukan cara kali silang.
Contoh :
1. Urutkan pecahan ²/₃ dan ⁵/₇
2. Urutkan pecahan ⁴/₅ dan ³/₈
Jawab:
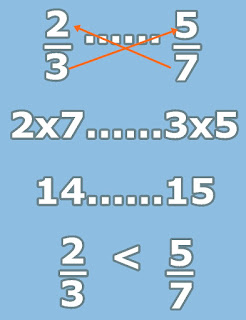
1. Kalikan 2 dengan 7, maka hasilnya 14. Letakkan di sebelah kiri.
Kalikan 5 dengan 3, maka hasilnya 15. Letakkan di sebalah kanan.
Karena hasil di sebelah kiri lebih kecil, artinya pecahan sebelah kiri nilainya lebih kecil.
Karena hasil di sebelah kiri lebih besar, artinya pecahan sebelah kiri nilainya lebih besar.
3. Mengurutkan lebih dari dua pecahan
Untuk mengurutkan lebih dari dua pecahan, bisa kita lakukan dengan beberapa cara. Kamu bisa memilih mana yang lebih mudah dilihat dari pecahan-pecahan yang diberikan.
a. Membandingkan antara dua pecahan
Contoh :
Urutkan pecahan ²/₃, ⁷/₈ dan ²¹/₂₅ dari yang terkecil
Jawab :
Bandingkan antara ²/₃ dan ⁷/₈
didapat 2x8 = 16 dan 7x3 = 21, maka ²/₃ lebih kecil dari ⁷/₈
Bandingkan antara ⁷/₈ dan ²¹/₂₅
didapat 7x25 = 175 dan 21x8 = 168, maka ⁷/₈ lebih besar dari ²¹/₂₅
Bandingkan antara ²/₃ dan ²¹/₂₅
didapat 2x25 = 50 dan 21x3 = 63, maka ²/₃ lebih kecil dari ²¹/₂₅
Kesimpulannya ²/₃ adalah pecahan dengan nilai terkecil dan ⁷/₈ terbesar
Urutan dari yang terkecil : ²/₃, ²¹/₂₅, ⁷/₈
b. Merubah ke bentuk desimal
Setiap pecahan dirubah ke bentuk desimal dengan tempat desimal yang sama.
contoh :
Urutkan pecahan ⁵/₈, ³/₄, ¹³/₂₀ dan ²²/₂₅ dari yang terbesar
Jawab :
⁵/₈ = 0,625 (tiga tempat desimal)
³/₄ = 0,75 = 0,750 (tiga tempat desimal)
¹³/₂₀ = 0,65 = 0,650 (tiga temat desimal)
²²/₂₅ = 0,88 = 0,880 (tiga tempat desimal)
0,880 > 0,750 > 0,650 > 0,625
Urutan dari yang terbesar ²²/₂₅ ; ³/₄ ; ¹³/₂₀ ; ⁵/₈
c. Menyamakan penyebut
Mengurutkan pecahan dengan menyamakan penyebut lalu diurutkan berdasarkan nilai pembilangnya. Menyamakan penyebut dengan merubahnya ke KPK (Kelipatan Persekutuan terKecil)nya.
contoh :
Urutkan pecahan ³/₅, ⁴/₁₅, ¹⁹/₃₀ dan ⁷/₁₀ dari yang terkecil
maka samakan penyebutnya menjadi 30
³/₅ = ¹⁸/₃₀
⁴/₁₅ = ⁸/₃₀
¹⁹/₃₀ = ¹⁹/₃₀
⁷/₁₀ = ²¹/₃₀
Urutan dari yang terkecil
⁸/₃₀ ; ¹⁸/₃₀ ; ¹⁹/₃₀ ; ²¹/₃₀
= ⁴/₁₅ ; ³/₅ ; ¹⁹/₃₀ ; ⁷/₁₀
4. Mengurutkan bentuk pecahan berbeda
Pecahan dapat berbentuk pecahan biasa, pecahan desimal, persen ataupun pecahan campuran. Untuk mengurutkan ataupun membandingkannya maka kita perlu mengubah setiap pecahan ke dalam bentuk yang sama.
a. Samakan ke bentuk pecahan biasa
contoh :
Urutkan pecahan ⁷/₂₀ ; 0,67 ; 55% dari yang terbesar
jawab :
Pecahan desimal dan persen diubah ke pecahan biasa
0,67 = ⁶⁷/₁₀₀
55% = ⁵⁵/₁₀₀
samakan penyebut (dalam soal ini 100)
³⁵/₁₀₀ = ³⁵/₁₀₀
Urutan dari yang terbesar
⁶⁷/₁₀₀ ; ⁵⁵/₁₀₀ ; ³⁵/₁₀₀
= 0,67 ; 55% ; ³⁵/₁₀₀
b. Samakan ke bentuk desimal
contoh :
Urutkan pecahan 38,5% ; ³/₈ ; 0,45 dan ⁹/₂₅ dari urutan terkecil
jawab :
38,5% = 0,385
³/₈ = 0,375
0,45 = 0,450
⁹/₂₅ = 0,360
Urutan pecahan dari yang terkecil 0,360 ; 0,375 ; 0,385 ; 0,450
= ⁹/₂₅ ; ³/₈ ; 38,5% ; 0,45
c. Jika ada pecahan campuran atau nilai satuan
Jika dalam beberapa pecahan yang diketahui dalam soal terdapat bentuk pecahan campuran atau pecahan yang memiliki nilai satuan, maka pisahkan pecahan tersebut. Pecahan-pecahan yang memiliki satuan dianggap memiliki nilai yang lebih besar.
contoh :
1. Urutkan pecahan ⁵/₈ ; 1 ⁵/₁₂ ; 0,6 dan 57% dari yang terkecil
2. Urutkan pecahan 2 ¹/₃ ; 89% ; 2,4 ; ⁴/₅ dari yang terbesar
3. Urutkan pecahan ⁸/₂₅ ; 2 ⁵/₉ ; 1,23 dan 2 ¹¹/₁₅ dari yang terkecil
jawab :
1. Dari soal, pecahan yang memiliki nilai satuan hanya 1 ⁵/₁₂. Maka pecahan tersebut adalah pecahan dengan nilai terbesar. Selanjutnya kita urutkan pecahan-pecahan yang lain dengan cara manapun yang kamu kuasai. Misalnya kita ubah ke bentuk desimal.
⁵/₈ = 0,625
0,6 = 0,600
57% = 0,570
Urutan yang dari yang terkecil 57% ; 0,6 ; ⁵/₈ ; 1 ⁵/₁₂
2. Pecahan yang memiliki satuan adalah 2 ¹/₃ dan 2,4. Karena satuannya sama-sama 2, maka bandingkan pecahannya yaitu ¹/₃ dan 0,4
¹/₃ = 0,3 jadi lebih kecil dari 0,4
2,4 > 2 ¹/₃
Pecahan yang tersisa adalah 89% dan ⁴/₅
89% = 0,89
⁴/₅ = 0,80
maka 89% > ⁴/₅
Urutan dari yang terbesar adalah 2,4 ; 2 ¹/₃ ; 89% ; ⁴/₅
3. Pecahan yang memiliki satuan adalah 2 ⁵/₉ ; 1,23 dan 2 ¹¹/₁₅
Yang terkecil adalah 1,23 karena satuannya 1 sedang yang lainnya 2.
Kita bandingkan pecahan dari 2 ⁵/₉ dan 2 ¹¹/₁₅
Urutan pecahan dari yang terkecil ⁸/₂₅ ; 1,23 ; 2 ⁵/₉ ;2 ¹¹/₁₅
Demikian uraian kami tentang cara mengurutkan pecahan dengan berbagai bentuknya. Semoga membantumu lebih memahaminya.
Kali ini kita akan membahas tentang cara mengurutkan bilangan pecahan. Mengurutkan bisa dari terkecil ke terbesar atau sebaliknya dari yang terbesar ke yang terkecil. Ya jika bilangan cacah tentu kita mudah mengurutkan dengan hanya melihat angkanya sekilas. Begitupun dengan bilangan bulat, selain melihat angkanya kita juga harus memperhatikan tandanya.
Dalam mengurutkan bilangan pecahan, kamu harus menguasai perkalian, pembagian, pemfaktoran dan menentukan KPK. Materi mengurutkan pecahan ini dipelajari di kelas 6 karena pada kelas-kelas sebelumnya kita sudah mempelajari pemfaktoran dan KPK tersebut.
Berikut cara-cara mengurutkan pecahan yang akan kita pelajari
1. Mengurutkan pecahan dengan penyebut yang sama
Perhatikan garis bilangan berikut !
Garis bilangan di atas menunjukkan bagian-bagian dari garis yang dibagi menjadi 9 ruas. Bisa kita lihat bagian-bagiannya adalah pecahan dengan penyebut 9. Pecahan-pecahan dengan penyebut yang sama akan terlihat polanya yang jelas, yaitu pecahan dengan nilai pembilang paling kecil berada di sebelah kiri garis bilangan. Artinya pecahan yang penyebutnya sama dapat diurutkan nilai terkecilnya adalah yang memiliki pembilang terkecil dan seterusnya.
Pecahan-pecahan dengan penyebut yang sama nilainya akan semakin besar jika pembilangnya makin besar.
2. Mengurutkan pecahan dengan pembilang yang sama
Pembilang dalam pecahan bisa dianggap juga sebagai pembagi. Jika suatu bilangan yang sama dibagi angka yang lebih besar tentu menghasilkan nilai yang lebih kecil.
Contoh:
8 artinya 8 : 8 = 1
8
8 artinya 8 : 4 = 2
4
8 artinya 8 : 2 = 4, dan
2
8 artinya 8 : 1 = 8
1
Bisa kita lihat bahwa semakin kecil penyebut atau pembagi, maka nilai bilangan akan semakin besar. Jadi bisa kita simpulkan bahwa, untuk pecahan-pecahan dengan pembilang yang sama nilainya akan semakin besar jika penyebutnya semakin kecil.
3. Mengurutkan dua pecahan
Jika dua pecahan yang akan diurutkan memiliki penyebut yang sama atau pembilang yang sama, maka aturan yang sudah dibahas sebelumnya berlaku. Tapi jika dua pecahan yang akan diurutkan memiliki pembilang maupun penyebut yang berbeda bisa kita lakukan cara kali silang.
Contoh :
1. Urutkan pecahan ²/₃ dan ⁵/₇
2. Urutkan pecahan ⁴/₅ dan ³/₈
Jawab:
1. Kalikan 2 dengan 7, maka hasilnya 14. Letakkan di sebelah kiri.
Kalikan 5 dengan 3, maka hasilnya 15. Letakkan di sebalah kanan.
Karena hasil di sebelah kiri lebih kecil, artinya pecahan sebelah kiri nilainya lebih kecil.
2. Kalikan 4 dengan 8, maka hasilnya 32. Letakkan di sebelah kiri.
Kalikan 3 dengan 5, maka hasilnya 15. Letakkan di sebalah kanan. Karena hasil di sebelah kiri lebih besar, artinya pecahan sebelah kiri nilainya lebih besar.
3. Mengurutkan lebih dari dua pecahan
Untuk mengurutkan lebih dari dua pecahan, bisa kita lakukan dengan beberapa cara. Kamu bisa memilih mana yang lebih mudah dilihat dari pecahan-pecahan yang diberikan.
a. Membandingkan antara dua pecahan
Contoh :
Urutkan pecahan ²/₃, ⁷/₈ dan ²¹/₂₅ dari yang terkecil
Jawab :
Bandingkan antara ²/₃ dan ⁷/₈
didapat 2x8 = 16 dan 7x3 = 21, maka ²/₃ lebih kecil dari ⁷/₈
Bandingkan antara ⁷/₈ dan ²¹/₂₅
didapat 7x25 = 175 dan 21x8 = 168, maka ⁷/₈ lebih besar dari ²¹/₂₅
Bandingkan antara ²/₃ dan ²¹/₂₅
didapat 2x25 = 50 dan 21x3 = 63, maka ²/₃ lebih kecil dari ²¹/₂₅
Kesimpulannya ²/₃ adalah pecahan dengan nilai terkecil dan ⁷/₈ terbesar
Urutan dari yang terkecil : ²/₃, ²¹/₂₅, ⁷/₈
b. Merubah ke bentuk desimal
Setiap pecahan dirubah ke bentuk desimal dengan tempat desimal yang sama.
contoh :
Urutkan pecahan ⁵/₈, ³/₄, ¹³/₂₀ dan ²²/₂₅ dari yang terbesar
Jawab :
⁵/₈ = 0,625 (tiga tempat desimal)
³/₄ = 0,75 = 0,750 (tiga tempat desimal)
¹³/₂₀ = 0,65 = 0,650 (tiga temat desimal)
²²/₂₅ = 0,88 = 0,880 (tiga tempat desimal)
0,880 > 0,750 > 0,650 > 0,625
Urutan dari yang terbesar ²²/₂₅ ; ³/₄ ; ¹³/₂₀ ; ⁵/₈
c. Menyamakan penyebut
Mengurutkan pecahan dengan menyamakan penyebut lalu diurutkan berdasarkan nilai pembilangnya. Menyamakan penyebut dengan merubahnya ke KPK (Kelipatan Persekutuan terKecil)nya.
contoh :
Urutkan pecahan ³/₅, ⁴/₁₅, ¹⁹/₃₀ dan ⁷/₁₀ dari yang terkecil
maka samakan penyebutnya menjadi 30
³/₅ = ¹⁸/₃₀
⁴/₁₅ = ⁸/₃₀
¹⁹/₃₀ = ¹⁹/₃₀
⁷/₁₀ = ²¹/₃₀
Urutan dari yang terkecil
⁸/₃₀ ; ¹⁸/₃₀ ; ¹⁹/₃₀ ; ²¹/₃₀
= ⁴/₁₅ ; ³/₅ ; ¹⁹/₃₀ ; ⁷/₁₀
4. Mengurutkan bentuk pecahan berbeda
Pecahan dapat berbentuk pecahan biasa, pecahan desimal, persen ataupun pecahan campuran. Untuk mengurutkan ataupun membandingkannya maka kita perlu mengubah setiap pecahan ke dalam bentuk yang sama.
a. Samakan ke bentuk pecahan biasa
contoh :
Urutkan pecahan ⁷/₂₀ ; 0,67 ; 55% dari yang terbesar
jawab :
Pecahan desimal dan persen diubah ke pecahan biasa
0,67 = ⁶⁷/₁₀₀
55% = ⁵⁵/₁₀₀
samakan penyebut (dalam soal ini 100)
³⁵/₁₀₀ = ³⁵/₁₀₀
Urutan dari yang terbesar
⁶⁷/₁₀₀ ; ⁵⁵/₁₀₀ ; ³⁵/₁₀₀
= 0,67 ; 55% ; ³⁵/₁₀₀
b. Samakan ke bentuk desimal
contoh :
Urutkan pecahan 38,5% ; ³/₈ ; 0,45 dan ⁹/₂₅ dari urutan terkecil
jawab :
38,5% = 0,385
³/₈ = 0,375
0,45 = 0,450
⁹/₂₅ = 0,360
Urutan pecahan dari yang terkecil 0,360 ; 0,375 ; 0,385 ; 0,450
= ⁹/₂₅ ; ³/₈ ; 38,5% ; 0,45
c. Jika ada pecahan campuran atau nilai satuan
Jika dalam beberapa pecahan yang diketahui dalam soal terdapat bentuk pecahan campuran atau pecahan yang memiliki nilai satuan, maka pisahkan pecahan tersebut. Pecahan-pecahan yang memiliki satuan dianggap memiliki nilai yang lebih besar.
contoh :
1. Urutkan pecahan ⁵/₈ ; 1 ⁵/₁₂ ; 0,6 dan 57% dari yang terkecil
2. Urutkan pecahan 2 ¹/₃ ; 89% ; 2,4 ; ⁴/₅ dari yang terbesar
3. Urutkan pecahan ⁸/₂₅ ; 2 ⁵/₉ ; 1,23 dan 2 ¹¹/₁₅ dari yang terkecil
jawab :
1. Dari soal, pecahan yang memiliki nilai satuan hanya 1 ⁵/₁₂. Maka pecahan tersebut adalah pecahan dengan nilai terbesar. Selanjutnya kita urutkan pecahan-pecahan yang lain dengan cara manapun yang kamu kuasai. Misalnya kita ubah ke bentuk desimal.
⁵/₈ = 0,625
0,6 = 0,600
57% = 0,570
Urutan yang dari yang terkecil 57% ; 0,6 ; ⁵/₈ ; 1 ⁵/₁₂
2. Pecahan yang memiliki satuan adalah 2 ¹/₃ dan 2,4. Karena satuannya sama-sama 2, maka bandingkan pecahannya yaitu ¹/₃ dan 0,4
¹/₃ = 0,3 jadi lebih kecil dari 0,4
2,4 > 2 ¹/₃
Pecahan yang tersisa adalah 89% dan ⁴/₅
89% = 0,89
⁴/₅ = 0,80
maka 89% > ⁴/₅
Urutan dari yang terbesar adalah 2,4 ; 2 ¹/₃ ; 89% ; ⁴/₅
3. Pecahan yang memiliki satuan adalah 2 ⁵/₉ ; 1,23 dan 2 ¹¹/₁₅
Yang terkecil adalah 1,23 karena satuannya 1 sedang yang lainnya 2.
Kita bandingkan pecahan dari 2 ⁵/₉ dan 2 ¹¹/₁₅
Urutan pecahan dari yang terkecil ⁸/₂₅ ; 1,23 ; 2 ⁵/₉ ;2 ¹¹/₁₅
Demikian uraian kami tentang cara mengurutkan pecahan dengan berbagai bentuknya. Semoga membantumu lebih memahaminya.









Komentar