POLA BILANGAN PART 1 : Matematika Kelas VIII MTs Muhammadiyah 1 Muntilan

-
 
POLA BILANGAN

Pola bilangan ganjil

  • Pola bilangan ganjil memiliki pola 1, 3, 5, 7, 9 ….
  • Barisan bilangan ganjil adalah 1,3, 5, 7, 9, …
  • Deret bilangan ganjil adalah 1 + 3 + 5 + 7 + 9 + ….
  • Rumus mencari suku ke ke-n adalah Un = 2n – 1
  • Rumus mencari jumlah n suku pertama adalah Sn = n2
  • Berikut adalah gambar pola dari bilangan ganjil
    pola barisan bilangan ganjil

Pola bilangan genap

  • Pola bilangan genap adalah 2, 4, 6, 8, 10, …..
  • Barisan bilangan genap adalah 2, 4, 6, 8, 10, ….
  • Deret bilangan genap adalah 2 + 4 + 6 + 8 + 10 + …..
  • Rumus untuk mencari suku ke-n adalah Un = 2n
  • Rumus mencari jumlah n suku pertama adalah Sn = n2 + n
  • Gambar pola bilangan genap adalah sebagai berikut
Pola Barisan bilangan genap

Pola bilangan segitiga

  • Pola bilangan segitiga adalah 1, 3, 6, 10, 15, 21, …..
  • Barisan bilangan segitiga adalah 1, 3, 6, 10, 15, 21, …..
  • Deret bilangan segitiga adalah 1 + 3 + 6 + 10 + 15 + 21 + …..
  • Rumus mencari suku ke-n adalah Un = ½ n (n + 1 )
  • Rumus mencari jumlah n suku pertama adalah Sn = 1/6 n ( n + 1 ) ( n + 2 )
  • Gambar pola bilangan segitiga adalah sebagai berikut
    pola barisan bilangan segitiga

Pola bilangan persegi

  • Pola bilangan persegi adalah 1, 4, 9, 16, 25, …..
  • Barisan bilangan persegi adalah 1, 4, 9, 16, 25, …..
  • Deret bilangan persegi adalah 1 + 4 + 9 + 16 + 25 + ……
  • Rumus mencari suku ke-n adalah Un = n2
  • Rumus mencari jumlah n suku pertama adalah Sn = 1/6 n ( n + 1 ) ( 2n + 1 )
  • Gambar pola bilangan persegi adalah sebagai berikut
    pola barisan bilangan persegi

Pola bilangan persegi panjang

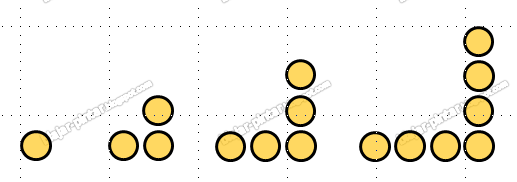
  • Pola bilangan persegi panjang adalah 2, 6, 12, 20, 30, ……
  • Barisan bilangan persegi panjang adalah 2, 6, 12, 20, 30, ……
  • Deret bilangan persegi panjang adalah 2 + 6 + 12 + 20 + 30 + …..
  • Rumus mencari suku ke-n adalah Un = n ( n + 1 )
  • Rumus mencari jumlah n suku pertama adalah Sn = 1/3 n ( n + 1 ) ( n + 2 )
  • Gambar pola bilangan persegi panjang adalah sebagai berikut
pola barisan bilangan persegi panjang

Pola bilangan segitiga pascal

  • Rumus mencari jumlah baris ke-n adalah 2n – 1
  • Gambar pola bilangan segitiga pascal adalah sebagai berikut
pola barisan bilangan segitiga pascal

Pola bilangan Fibonacci

  • Pola bilangan fibanocci adalah pola bilangan dimana jumlah bilangan setelahnya merupakan hasil dari penjumlahan dari dua bilangan sebelumnya.
  • Pola bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, 21, 34, …..
  • 2 diperoleh dari hasil 1 + 1 3 diperoleh dari hasil 2 + 1, 5 diperoleh dari hasil 3 + 2 dan seterusnya
  • Rumus mencari suku ke-n adalah Un = Un – 1 + Un - 2

Pola bilangan pangkat tiga

  • Pola bilangan pangkat tiga adalah pola bilangan dimana bilangan setelahnya merupakan hasil dari pangkat tiga dari bilangan sebelumnya
  • Contoh pola bilangan pangkat tiga adalah 2, 8, 512, 134217728, …..
  • Keterangan : 8 diperoleh dari hasil 2 pangkat tiga, 512 diperoleh dari hasil 8 pangkat tiga, dan seterusnya

Pola bilangan aritmatika

  • Pola bilangan aritmatika adalah pola bilangan dimana bilangan sebelum dan sesudahnya memiliki selisih yang sama.
  • Contoh pola bilangan aritmatika adalah 2, 5, 8, 11, 14, 17, ….
  • Suku pertama dalam bilangan aritmatika dapat disebut dengan awal ( a ) atau U1, sedangkan suku kedua adalah U2 dan seterusnya.
  • Selisih dalam barisan aritmatika disebut dengan beda dan dilambangkan dengan b.
  • Karena bilangan sebelum dan sesudahnya memiliki selisih yang sama, maka b = U2 - U1 = U3 – U2 = U4 – U3 = U5 – U4 = U6 – U5 = 3
  • Rumus mencari suku ke-n adalah Un = a + ( n – 1 ) b
  • Rumus mencari jumlah n suku pertama adalah Sn = n/2 ( a + Un ) atau Sn = n/2 ( 2 a + ( n – 1 ) b )
 
 Sumber: http://sapakabar.blogspot.co.id/2014/11/macam-macam-pola-barisan-bilangan-dalam-matematika.html

Komentar

Posting Komentar

Postingan populer dari blog ini

Koordinat Kartesius - Posisi Titik Terhadap Titik dan Garis : Kelas VIII Matematika MTs Muhammadiyah 1 Muntilan

-
Gambar
  Kalian yang saat ini duduk di bangku kelas 8 mungkin tak asing lagi dengan koordinat cartesius. Istilah Cartesius digunakan untuk mengenang ahli matematika sekaligus filsuf asal Prancis, Descartes, yang memiliki peran besar dalam menggabungkan aljabar dan geometri. Cartesius sendiri merupakan bentuk latin dari Descartes. Pada tahun 1637, dalam salah satu karyanya,  Discourse on the Method,  Descartes memperkenalkan ide baru untuk menggambarkan posisi titik atau objek pada sebuah permukaan, dengan menggunakan dua sumbu yang bertegak lurus antar satu dengan yang lain. Kemudian lewat tulisannya yang lain,  La Géométrie , ia pun memperdalam konsep-konsep yang telah dikembangkannya itu. Dalam Matematika, sistem koordinat cartesius digunakan untuk menentukan posisi titik pada bidang koordinat. Penulisannya sendiri ditandai dengan kurung kurawal dan dipisahkan dengan koma. Sebagai contoh (x, y), dimana x disebut absis, dan y disebut ordinat. Dua sumbu koordinat dapat diperoleh dengan cara m
Baca selengkapnya

Materi Skala dan Perbandingan Kelas 7 SMP

-
Gambar
Berbicara soal skala pasti yang teringat skala peta, bagaimana sih pembacaan skala pada peta ? perhatikan uraian berikut : Sebuah desain rumah digambarkan dengan skala 1 : 50, arti dari skala 1 : 50 yaitu setiap jarak satu centimeter pada gambar mewakili 50 centimeter jarak sesungguhnya. Jika panjang rumah pada gambar desain ditunjukkan dengan jarak 10 cm maka panjang rumah yang sesungguhnya adalah 10 x 50 cm = 500 cm. Dari uraian tadi dapat ikita tarik sebuah kesimpulan mengenai pengertian dari skala. Skala a dalah perbandngan antara jarak pada gambar dengan jarak sesungguhnya. Skala biasanya digunakan pada denah lokasi, peta, dan rancangan benda. Contoh penulisan skala : 1 : 20.000, 1 : 15.000, dan 1 : 1.750.000 Rumus Skala Contoh soal skala : Sebuah peta dengan skala 1 : 25.000, berapakah jarak sesungguhnya jika pada peta ditunjukkan dengan jarak 4 cm. jawab : jarak pada peta 4 cm jarak sebenarnya adalah 4 x 25.000 cm = 100.000 cm Bentuk-bentuk Pe
Baca selengkapnya

CONTOH SOAL DAN PEMBAHASAN POSISI GARIS TERHADAP GARIS : KOORDINAT KARTESIUS : MATEMATIKA : KELAS VIII : MTs MUHAMMADIYAH 1 MUNTILAN

-
Gambar
  CONTOH SOAL 1 Gambarlah garis l yang melalui titik A (3, -5) yang tidak sejajar dengan sumbu-X dan tidak sejajar dengan sumbu-Y ! Pembahasan : Gambar garis l yang melalui titik A (3,-5) yang tidak sejajar dengan sumbu-X dan tidak sejajar dengan sumbu-Y adalah sebagai berikut. Garis l pada bidang koordinat kartesius CONTOH 2 Gambarlah garis m dan n yang saling sejajar tapi tidak tegak lurus dengan sumbu-X dan sumbu-Y ! Penyelesaian : Berikut garis m dan n yang saling sejajar tapi tidak tegak lurus dengan sumbu-X dan sumbu-Y. Garis m, n pada bidang koordinat kartesius CONTOH SOAL 3 Diketahui titik A (3, 2 ), B (3, -6 ), C (-5, 2 ) a). Jika dibuat garis melalui titik A dan B, bagaimana kedudukan garis tersebut terhadap sumbu-X dan sumbu-Y b). Jika dibuat garis melalui titik A dan C, bagaimana kedudukan garis tersebut terhadap sumbu-X dan sumbu-Y c). Jika dibuat garis melalui titikk B dan C, bagaimana kedudukan garis tersebut terhadap sumbu-X dan sumbu-Y Penyelesaian : Langkah 1 Gambarl
Baca selengkapnya